Parallelizing A Generalized Neural Network
Summary
We are going to implement a generalized neural network (defined below) on NVIDIA GPUs with CUDA. Our network is different from a traditional neural network in two ways: 1) it is a directed acyclic graph consisting of many small matrix operations, instead of a few large ones; 2) computational units in the graph can be added (or pruned) dynamically during training. We observe that this type of neural network, while theoretically interesting, is rarely seen in literature, partly due to the lack of an efficient parallel implementation.
Backround
Neural Networks (NN) have seen rapid development in recent years, with successful applications in areas from computer vision to natural language processing. However, traditional neural networks all have a layered structure (Figure 1), which is a special case of network. We relax this requirement to allow networks with any acyclic graph structure (Figure 2). We call them Generalized Neural Networks. In Figure 2, each circle is akin to a layer (a neuron group) in a traditional neural network, with a fixed number of neurons. However, instead of arranging the neuron groups as layers, we allow them to follow any graph structure. We note that traditional neural networks are a special case of this structure. For example, using our definition, Figure 1 is a linked list of 10 neuron groups (including one input neuron group); each of the dense neuron groups has 4096 neurons.
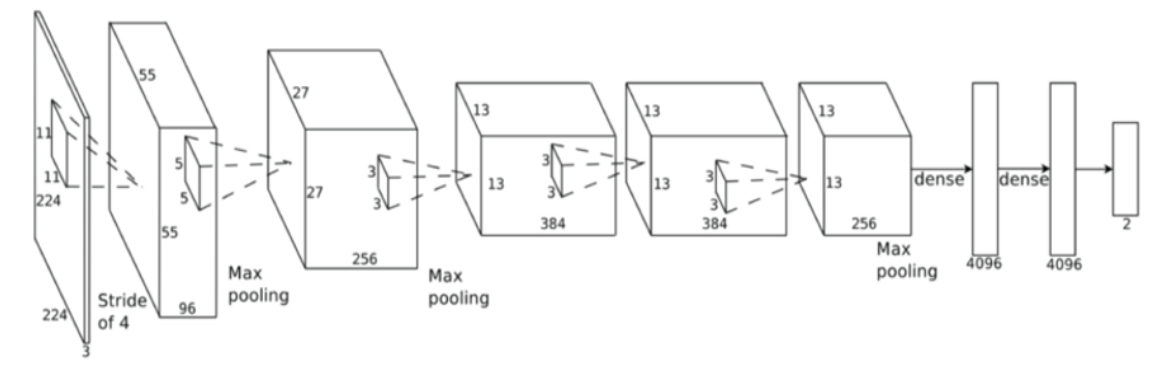
Figure 1: An example of a layered neural network.
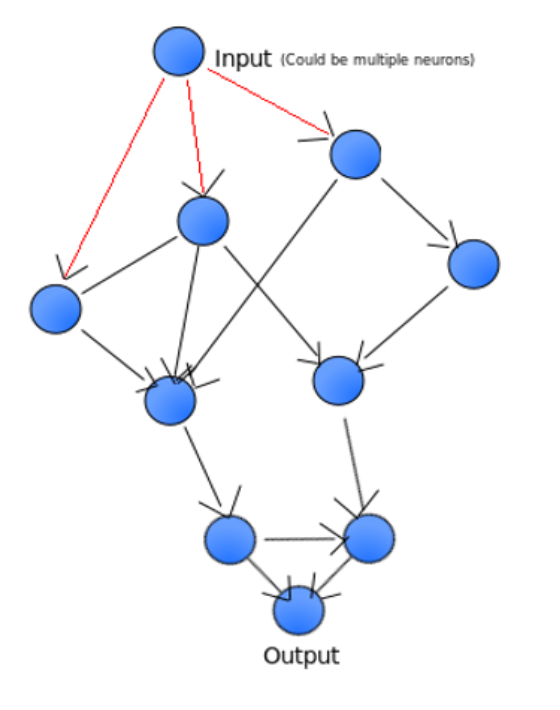
Figure 2: A Generalized Neural Network.
We intend for our network to have many small neuron groups, instead of a few large layers. Note that most deep learning toolkits (such as PyTorch or Tensorflow) are optimized for the latter case, and do not perform well in the former. We also stress that our network is not a Graph Neural Network, which has graphs as the input instead of the network structure.
It will be difficult to manually specify the structure of a large generalized network. Hence, we propose the following mechanism to dynamically add neurons during training. When the standard deviation of the gradients of a neuron group is larger than a given threshold, it will undergo a depth- or widthwise duplication (Figure 4). (We will also choose the neuron group closest to the input for duplication if multiple consecutive neuron groups are eligible.) This allows forming any network structure from a single neuron group.
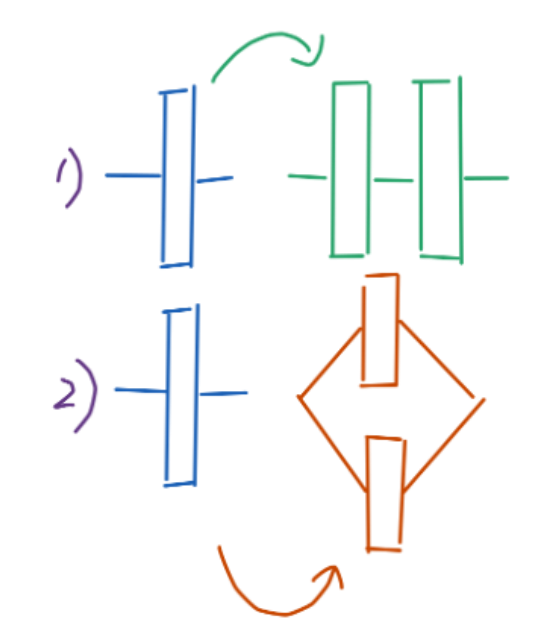
Figure 4: Dynamically duplicated neuron groups.
Similar to modern neural networks, our proposal naturally benefits from parallelization due to its large size of mostly independent neuron groups. The large number of neuron groups and small number of neurons, as well as the network modification rules, add challenge to parallelization and make parallelization of this problem non-trivial. Despite the motivation of this project from machine learning, we will prioritize finding good parallelization strategies and trying algorithms that have impacts on parallelism (discussed in sections below).
We are going to parallelize our implementation with CUDA. Computation of neuron groups and neurons in one group can both be parallelized. Our DAG network structure and dynamic network modifications make our network more difficult to parallelize than traditional neural networks.
Challenges
● Parallelism must preserve DAG dependency (unlike traditional NN which is more like a single linked list).
● Adding a neuron group will break the dependency graph. It will be difficult to parallelize inserting a neuron group into an array at a location.
● Multiple processors can add neuron groups at the same time.
● Work is unbalanced when duplicating (neuron groups that are duplicating have more work) and leads to divergent execution (more branches).
● Communication to computation ratio depends on the size of each neuron group.
● Cache locality (memory access in naive graphs can be very cache unfriendly - might need to semi-dynamically rearrange neuron groups).
● Duplications happen at the earliest neuron in the DAG - need to communicate.
● Criteria as shown above requires reduction to mean.
● The maximum number of neuron groups is a global limit - needs to synchronize when this limit is reached.
● Dynamic graph - it will be difficult to use tools like graphlab.
Resources
We plan to conduct our experiments on GPUs. We will use GHC machines with NVIDIA GeForce RTX 2080 B GPUs. We will start from scratch but use existing neural network implementations as a reference [1].
Goals and Deliverables
Plan to Achieve
We note that the goal of this project is not to search for a training mechanism that produces a good result. Instead, we keep the duplication criteria as simple as possible, and strive for a good parallel implementation. In particular, we will start by implementing the following algorithm:
● We start with linear (dense) layers only with ReLU activations.
● In the forward pass, each neuron group takes input from N other neuron groups and sends its output to M neuron groups.
● In the backward pass, each neuron group takes the gradients from M neuron groups, calculates the standard deviation of the gradients, and marks the neuron for duplication if the aforementioned criteria is met.
● If multiple consecutive neuron groups are marked for duplication, we duplicate the one closest to the input.
We will benchmark our parallel implementation against a serial implementation and an implementation using PyTorch. Note that PyTorch is not optimized for numerous small layers and dynamic network modification; we expect some improvement over the status quo.
Hope to Achieve
● We don’t have to use dense layers. CNNs and attentions will also work.
● Different criteria other than standard deviation for adding neuron groups - this requires theoretical research.
● Recurrence - loops in the graph.
● Apart from adding neuron groups, we can also prune neuron groups.
In case the work goes more slowly than expected, we will prioritize implementing the depthwise duplication algorithms as they are of the most theoretical curiosity, allowing for dynamically sizing the depth of a neural network.
Demo
We will show the training process of our network on an example dataset. An animated graph visualization throughout the training will be provided to help gain insight into this network structure.
We will also show the speedup of our parallelized implementation against a serial implementation and a PyTorch implementation baseline, as well as a comparison on the accuracy between our model and a traditional NN.
Platform Choice
We have thousands of neuron groups with several neurons each to parallelize. Most neuron groups perform the same instructions. Hence, we will use CUDA to allow for the massive, small-task parallelization and take advantage of SIMD execution model.
Schedule
11/3: Project proposal.
11/8: Data structures, forward pass.
11/15: Forward/backward passes. (Static network structure.)
11/22: Depthwise duplication. Project milestone report.
11/29: Widthwise duplication and optimizations.
12/6: More optimizations. For example, trying different data layouts, different synchronization strategies for network modification, parallel topological sort, and push vs. pull communication strategies.
12/9: Final project report.
References
[1] Implementing a Neural Net in CUDA From Scratch, Parts 1-6. https://medium.datadriveninvestor.com/implementing-a-neural-net-in-cuda-from-scratch-part-1-introduction-9cd7f63573a7
Related Work
- A related work that considers dynamically modifying the network on the neuron level (mostly pruning): https://rohitbandaru.github.io/papers/CS_6787_Final_Report.pdf
- Widening neural networks (considers adding neurons) https://arxiv.org/pdf/1511.05641.pdf
- A blogpost that discusses expansion, splitting, and duplication https://hackernoon.com/dynamically-expandable-neural-networks-ce75ff2b69cf
- Dynamic NN survey paper. It considers changing the network structure based on input (e.g. by switching parts of a network on/off): https://arxiv.org/pdf/2102.04906.pdf